61.

If  =100, then find the value of x.

         a. 1000                         b. 100                           c. 10                 d. None of these

62.

Five years ago, a man’s age was 7 times that of his son’s age. Five years later, the son’s age would be one-third that of his father’s age. Find the present age of the father.

         a. 40                             b. 45                             c. 50                 d. None of these

63.

While solving a quadratic equation of the form x² +  bx + c = 0, a student took the coefficient of x incorrectly as -13 instead of -15 and the roots were found to be 4 and  9.  Find the correct roots of the equation.

         a. 5, 7                           b. 6, 9                           c. 7, 8               d. None of these

64.

Find the sum of all those integers between 250 and 750 which on being divided by 6 leave a remainder 2 in each case.

         a. 40,000                       b. 40,500                      c. 41,500           d.  None of these

65.

A luncheon is arranged for 20 people. They were seated along the two sides of a long table with 10 chairs on each side.  Five men wished to sit on one particular side and three on the other side.  In how many ways can the 20 persons be seated?

         a. 792(10!)²                    b. (10!)²              c. 863(10!)         d. None of these

66.

There are 20 points in a plane of which 8 are collinear.  Find the number of triangles that can be formed from these 20 points.

         a. 1140                         b. 1084                         c. 964               d. None of these

67.

There are 8 men and 6 women who are eligible for being included in a committee. If the committee must have atleast one female member, then in how many ways can the committee be formed?

a. 

b. 

            c.   Data insufficient

            d.   None of these

Directions for questions 68 to 76:

In a game of snooker there are 15 red balls and 6 coloured balls. The coloured balls are yellow, green, brown, blue, pink and black which have to be potted according to the following rules.

A player is eligible to pot a coloured ball only after potting a red ball.  The first pot of any player is always a red ball and a coloured ball must be potted between any two red balls.  A player can never pot two balls is one stroke.  A coloured ball is replaced back on the table after it is potted while the red ball once potted cannot be replaced. Once all the red balls are exhausted, the coloured balls are potted in the same order as mentioned above. For every red pot a player gets 1 point and the points for the coloured balls are yellow-2, green-3, brown-4, blue-5, pink-6 and black-7. For every foul, a player is fined 4 points.

68.

Find the number of ways in which a player can pot all the balls in one chance.

           a. 720                      b. 721                       c. 680               d. None of these

69.

Find the maximum number of points that a player can score if he doesn’t commit any foul.

           a. 120                      b.130                        c.147                d. Cannot be determined

70.

Find the minimum number of points that a player can score if he has to clear the table without committing any foul.

           a. 45                       b.  72                         c.  80                d.  None of these

With the aim of drawing the game, two friends Rajeev and Sanjeev play snooker with a rule that each one of them must pot only 2 balls at a time and they decide that they have to pot the same colours till they can do so.

71.

If Rajeev pots a yellow ball for his 15^th red ball which coloured ball can Sanjeev pot?

           a. Blue and Pink                                b. Pink and black
           c. Yellow and green                           d. Cannot be determined

72.

If Sanjeev pots a green and brown ball in his turn, then which of the following should be left out by Rajeev?

           a. yellow and black                            b.  pink and yellow
           c. yellow and blue                              d.  None of these

73.

Which of the following must necessarily be true?

           a. Sanjeev pots yellow and green         b.   Sanjeev pots pink and yellow
           c. Sanjeev pots yellow and brown        d.    Sanjeev does not pot blue and black

74.

If Sanjeev suddenly decides to win the game then which of the following coloured balls should Sanjeev pot to eliminate the chances of Rajeev winning?

           a.  Pink and Black                              b. Brown and Pink
           c.  Yellow and Black                           d. Brown and Black 

75.

If Rajeev suddenly decides to win then which of the following coloured balls should be definitely pot ?

           a. Blue and Pink                               b. Blue and Black
           c. Pink and Black                             d. None of these

76.

Two dice are thrown simultaneously.  What is the probability of getting a total score of atleast 9?

           a.                      b.                        c.                  d.  None of these

Directions for questions 77 and  79: 

A company manufactures a machine (m) which consists of two parts A and B.  It is found that in a lot of 10,000 units of part A, 800 are defective and in a lot of 20,000 units of part B, 400 are defective.

77.

What is the maximum number of units of machine (m) that could be defective in a lot of 1 lakh units?

           a. 8000             b. 2000                         c. 10000            d.    None of these

78.

What is the minimum number of units of machine (m) that could be defective in a lot of 1 lakh?

           a. 8000                b.  2000                                 c. 10000               d.    None of these

79.

What is the probability that the machine will not be defective?

           a. 0.6               b. 0.7                            c. 0.8                 d. 0.9

80.

A bag contains 7 blue balls and 5 green balls.  If 4 balls are drawn at random then what is the probability that of the 4 balls drawn, 2 are blue and 2 green?

           a.            b.                          c.                d .None of these

81.

Srinivas lost some cards from a pack of 52 cards.  He noticed that, of the remaining, 8 were spades, none wore diamonds, and there were 7 times as many clubs as hearts.  How many cards has he lost?

           a. 36                b. 35                             c. 34                 d. 37

82.

Ramesh and Arvind operate a joint account on a daily basis.  There was Rs.60, 000 in the account on the 1^st of January and Ramesh deposits Rs.1, 500 and with draws Rs.900 everyday.  Similarly, Arvind also withdraws Rs.1800 and deposits a certain amount.  If the balance in the account on the 10^th of January was still Rs.60, 000, then what was the amount deposited by Arvind everyday?

           a. Rs.1000                    b.  Rs.1400                   c. Rs.1200                d. Rs.1100

83.

Arts students and Commerce students combined can finish an assignment in eight days, while the Arts students alone can do the same assignment in nine days.  Both the group of students started the assignment together.  At half way, the Arts students entered into a fight with the Commerce students and the latter group was forced to finish the work alone.  What was the total duration of the assignment?

           a. 42 days                    b. 40 days                     c. 39 days                d. 36 days

84.

Sandeep won Rs.402 in a lottery.  He spent 1 rupee on a gift for each of his children.  He then distributed the balance among his children equally, in one rupee notes.  If his sons have 3 sisters, then how many rupees did each child get?

           a. 12                            b. 15                             c. 11                       d. 20

85.

If Richard covers a distance of 0.4 km in 15 minutes while going to college, he reaches his college 6 minutes late.  If he doubles his speed, he is 6 minutes early to the college.  What is the distance between his house and his college?

           a. 0.64 km                    b. 1 km                         c. 0.5 km              d. None of these

86.

The proprietor of “Cox Wines” shop removes 20 liters of brandy from a cask containing 100 litres and added back the same quantity of bear. The shop is very famous for alcohol adulteration.  On finding that inspectors from Food Quality Department are going to come for inspection, the proprietor of the shop removes 20 litres from the cask and added back 20 litres of brandy to it.  What is the present ratio of brandy to beer in the cask now?

           a. 100:1                        b. 84:16                        c. 80:20                  d. 64:16

87.

A second grade quality cooking oil of 58 litres was processed and found to be containing 25% of impurity. After processing completely, it yielded 50 litres of the first grade oil.  Find the percentage of impurity in the first grade oil.

         a. 12%                           b. 11%                          c. 13%                   d. 11.5%

88.

Anand passed his examination with 530 marks having scored 6% above the minimum.  If Srikant had obtained 700 marks, by what percentage would he have been above the minimum?

         a. 40                              b. 42                              c. 50                      d. 52

89.

The average weight of each girl in a class of 59, was 40 kg.  When one girl left the class, the average reduced by 200 gm.  Find the weight of the girl who left the class.

         a. 51.6 kg                       b. 55.3 kg                       c. 50kg                  d. 49 kg

90.

A mixture of alcohol and water contains 45% alcohol by weight.  Fifty grams of water is added to 100 grams of mixture.  What percentage of alcohol by weight is there in the new mixture?

         a. 25                               b. 29                              c. 30                      d. 32

91.

Alloys X and Y contain gold and copper in the ratio 5:2 and 3:4 respectively.  If equal weights of the two alloys are melted to form a third alloy Z,  then find the ratio of gold and copper in alloy  Z?

         a. 3:4                              b. 4:3                            c. 1:1                      d. 4:7

92.

18 students begin  to work together on a project, but after some days, 6 of them leave.  As a result, the project which should have been completed in 44 days is completed in   55 days. How many days after the commencement of the project did the 6 students leave?

         a. 23                               b. 20                             c. 22                        d. 19

93.

Venkat can build a wall in 6 days while Bhima can break it in 3 days. After Venkat had worked for 4 days, Bhima joined him and together they were on the job for 2 days.  In how many days can Venkat alone build the remaining part of the wall?

          a. 4                               b. 6                               c. 5                          d. 3

94.

Two pipes can fill a tank separately in 10 minutes and 15 minutes respectively.  Both the pipes are opened together for a certain time but being clogged only  of full quantity of water flows through the former and only  through the latter pipe. After some time, the obstacles in the pipe got cleared and the tank got filled in 3 minutes from that moment.  How long was it before the full flow began?

           a. 3.75 min                    b. 2.5 min                      c.  4 min                   d. 3 min

95.

A father left a will of Rs.84,000 to be divided  between his two sons aged 10 years and 15 years such that they may get equal amount when each attains the age of 18 years.  If the money is reckoned at 20% p.a, interest being compounded yearly, find the approximate amount that the 15 year old son received at the time of the will.

           a. Rs. 32000                  b. Rs. 52000                  c. Rs. 60000              d. Rs. 34000

96.

Gupta and sons is a business started with an initial investment of Rs.3, 20,000.  In the first year, it incurred a loss of 5%.  During the second year, it earned a profit of 20% , which in the third year was 12.5%. Calculate the net profit for the period of 3 years, if the proprietors of the company did not take any money from the business during that period.

           a. Rs. 90000                  b.  Rs. 90400                 c. Rs. 89400              d. Rs. 90500

97.

The odds that Kumar speaks the truth is 6:5 and odds that Bhanu speaks the truth is 8:7.  In what percentage of cases are they likely to agree with each other on an identical point?

           a. 48                             b. 50                            
           c. 46                             d. They can never agree with each other

98.

A cone is 1200 cm high and its slant height is inclined at 30⁰ to the horizontal.  Find the area of its curve surface.

           a.1567 m²                     b.1500 m²                      c. 1490m²                d. 1497 m²

99.

A field in the form of an isosceles triangle is levelled at the rate of Rs.5 per sq. m.  If the total cost of levelling was Rs.300 and the unequal side is 10 m long, then find the total number of poles required for fencing the field if the distance between any two poles should be 1 m and all the three vertices must have poles?

           a. 30                             b. 33                             c. 36                   d.  None of these

100.

PR is the diameter of a circle and also a diagonal of a quadrilateral PQRS inscribed in the circle.  If PQ =7cm, QR = 24cm, and RS =15cm, then find the approximate area of the portion of the circle excluding the quadrilateral.

          a. 491 sq. cm                b. 257 sq. cm                  c. 329 sq. cm        d. None of these

101.

A circle is inscribed in an n-sided regular polygon.  If the radius of the circle and the side of the polygon bear the ratio :2, then which of the following polygons can it be?

           a. Pentagon                   b. Hexagon            c. Heptagon      d. Cannot be determined

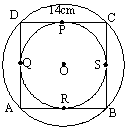
102.

In the following figure, if the side of the square is 14 cms then find the area of the region between the concentric circles.

           a. 154sq. cm                 b. 308 sq. cm            c. 385 sq. cm            d.  None of these

103.

In the given figure O1 and O2 are the centre of the circles. Find the area of the shaded region

         a.  sq. cm                                   b.   sq. cm             

         c. sq. cm                                   d. None of these

104.

Two solid cubes of sides 10cm and 9 cm are melted and reshaped into two cubes with integral sides of different measurements.  Find the cost of painting all the faces of the two cubes at the rate of 50 paise per sq.cm.

         a. Rs.375                     b. Rs.395                    c. Rs.435                  d. None of these

105.

An 8 cm cube is cut into 1cm cubes.  Find the percentage increase in the total surface area.

        a. 500%                       b. 600%                      c. 700%                    d.  900%

106.

In mid-summer, a thirsty crow searching for water finds a spherical pot of water which is half full to a height of 42 cm.  What is the minimum number of spherical pebbles of diameter 4cm must the crow drop into the pot if it has to quench its thirst considering that it can reach for water to a depth of 7 cm.

        a. 9261                         b. 9621                       c. 9629                     d.  None of these

107.

Find the area of LMN if X and Y are the midpoints of MN and LX respectively and area of NYX is 16 sq.cm.

         a. 64 sq. cm.                b. 32 sq. cm.               c. 48 sq. cm.             d. None of these

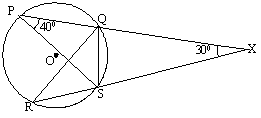
108.

Consider the adjoining figure and state which of the following is true

         a. QS = RS                  b.  QS < RS                  c. QS> RS               d. None of these

109.

Find the value of

         a. e³                           b. 3^e                            c. e^-3                      d. None of these

110.

If   and tan = 4,  then find the value of g.

         a.                            b.                            c.                     d.

Directions for question 111 to 115

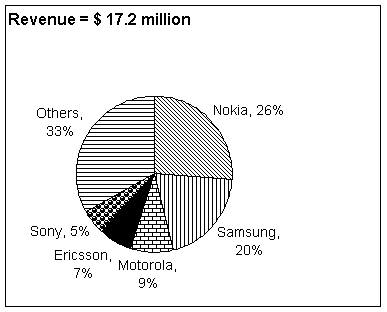
Study these pie-charts and answer the following questions. The first pie chart shows the total sales revenue from the sale of mobile phones and the second pie chart shows the volume sold by each company in 2001.

,

111.

For the year 2001, approximately how many more mobile phones did Sony sell than Samsung?

         a. 65,000                     b. 71,000                    c. 73,000                  d. 81,000

112.

For the year 2001, average unit sale price of a Nokia mobile phone was approximately

        a. $140                        b. $70                        c. $240                     d.  $260

113.

For the year 2001, which of the following companies realized the lowest average unit sale price for their mobile phone?

         a. Nokia                       b. Sony                      c. Ericsson                d.  None of these

114.

What is the approximate ratio of average unit price of Nokia to Motorola?

        a. 7 : 5                        b. 7 : 3                       c. 3 : 7                     d. 5 : 7

115.

Which of the following statements is false?

a. The average unit price of all the models is $28
b. The average unit sale price of Samsung $30
c. The market share (value wise) of other brand is $5.68 million
d. The market share (piece wise) of other brand is 11,500 units

Directions for questions 116 to 120

Following tables show the number of students of a college who took the tests in different subjects during the given years and the number of students who passed the tests:

116.

What is the ratio of the lowest pass percentage to the highest pass percentage in any ofthe subjects in any of the given years?

         a. 3 : 5                          b. 3 : 4                             c. 4 : 3              d. None of these

117.

Find the ratio of the percentage of students who failed in Physics in the year with the worst result in Physics to the percentage of students passed in Computer Science in the year with  the best results in Computer Science.

        a. 5 : 13                        b. 6 : 7                             c. 5 : 12            d. None of these

118.

What is the average pass percentage of the students of Statistics over the period 1997 to 2001?

         a. 74.1%                       b. 76.2%                           c. 75.1%           d. None of these

119.

What is the ratio of average pass percentage of Chemistry to Mathematics over the given period?

        a. 1.5 : 1                       b. 1 : 1.5                          c. 1 : 1              d. None of these

120.

What is the average percentage of students in Physics who failed over the given period?

         a. 20%                          b. 23%                             c. 25%              d. None of these